
Volume determination and extreme surface run off
Overview of methods to determine minimum, mean and maximum streamflow.
Information on this tool
Author: Dick Bouman, Aqua for All Rainwater Harvesting Workgroup
Version: 27 May 2009

Contents
1 Introduction
2 Flow determination
2.1 Flow measurements
2.2 Indirect flow determination
3 Flow characterization
4 Minimum flows
5 Annual flows
6 Floods
1 Introduction
Purpose
Mean annual flow in a stream as input for storage and recharge
Minimum flows (and length of non-discharge period for storage volume requirement
Maximum flows for storm water spill way capacity, erosion protection and retention capacity
Definition and Units (metric)
Flow is volume of water (litre or dm3; m3) that passes a (cross-)section of a stream in a unit of time (sec)
Discharge expressed as Q (l/s or m3/s); velocity as v ( m/s ); cross section as A (area; m2 or dm2)
Q = v*A (m/s*m2= m3/s; or dm/s* dm2 = l/s)
Cross-sectional area (A): the area of the section perpendicular to the direction of flow.
Wetted perimeter (P): the distance around the edge of the cross-section which is touched by liquid, excluding the water surface itself??)
Hydraulic radius (R): the ratio of the cross-sectional Area to the wetted perimeter. (A/P)
River regimes
Perennial/continuous: year round water
Seasonal: Only water in wet season (and limited period thereafter)
Intermittent: Only water during/after rain storms
Issues
Flow determination
Flow regime/ variations
annual flows (minimum – mean – maximum)
length ‘dry season’
minimum flows (extremes)
maximum flows
References
Very few publications/books are freely available/downloadable from internet.
Many publications have problem of using US units and not SI unit system.
Harvey A. (1993), Micro-hydro design manual, a guide to small-scale water power schemes, IT-Publications, ISBN 1 85339 103 4
Meijerink A.M.J. (1970/1973) Photo-interpretation in hydrology, a geomorphological approach (ITC text book)
Petts G and Foster I. (1985) Rivers and landscape, Edward Arnold Publishers, ISBN 0-7131-6433-6
Rasmussen (20xx) Quantative hydrology, University of Georgia/Athens (18/5/2009)
Queensland Department of Main Roads (2003) Road design manual, especially chapter 3 (Hydrology and design criteria) (25/5/2009)
Idem: suggestions for corrections (2007)
Waterlines (1991) Discharge measurements and estimates (Technical Brief No 27)
Websites
EngineeringToolbox (e.g. conversion program SI units; subject search)
Several other ‘calculation aids’
Search engines such as als Google; ScienceDirect
2 Flow
determination
One may determine the discharge/flow in a stream in different ways, mostly starting from the formulae Q = v*A. Distinguished methods are:
Measuring Volume/time (‘bucket method’)
Outflow curve of a full pipe as a measure of discharge
Measuring v and A (float, propeller)
Measuring by salt dilution (instant gulp, or constant salt inflow)
Using Q/h characteristics of calibrated weirs and/or flumes
Manning formulae, using stream levels/cross section characteristics, roughness of stream bottom and gradient
By correlation with similar streams with known flow (or flow characteristics)
By empirical formulae (using area of catchment, rainfall, run off coefficient and may be other catchment parameters), sometimes presented by graphs
The two latter methods are mostly not used for instant discharge determination, but for general characteristics, like mean annual discharge, mean annual flood or extreme floods. They will only be dealt with under the specific headings.
2.1 Flow measurements
Bucket method. Volumetric measurement for small volumes: bucket/container filled in time (e.g. 20 l in 4 seconds: Q=5 l/s). Stream flow can be concentrated for more accurate measurement.
If the discharge is too high for accurate measurement with a bucket, the flow can be concentrated in a horizontal pipe. For a full pipe of at least 1 m length, the outflow curve of the pipe is a measure for the discharge. If x is the distance in dm from the pipe mouth to the point where the flow is curved 1 dm (= y), then Q = c * A * x * (9.81/2y)0.5, where c is a coefficient in range of 1 – 1.1 A is the area of pipe cross section (dm2) and Q is in l/sec. (Reference: Waterlines)
Float method. Rapid discharge measurement by one velocity measurement in central current of stream : Q = C * vmax * A. C is dependent on channel form and roughness. (see table). Velocity can be determined by letting float a small object in the centre of the current; or by measuring the time a color tracer takes over a longer distance with rather uniform cross section.
Correction factor for stream velocity for float method (Harvey, 1993)
-
Character of stream bed
Correction factor
Concrete channel, rectangular, smooth
0.85
Large and slow clear stream
0.75
Small regular stream; smooth
0.65
Shallow turbulent stream
0.45
Very shallow rocky stream
0.25
Example: in a channel with a depth of 2 dm and width of 4 dm (A=8 dm2), a small leaf is transported by the main current in 5 seconds over 10 dm (v = 2 dm/s). Channel is rectangular (C= 0.85 ); then Q = C * v * A = 0.85 * 2 * 8 = 14 l/s);
Accurate discharge measurement with velocity measurements at different points in the section, using a propeller (‘Ott meter’). Application for stream beds with rather smooth flow distribution. Rather complicated calculation with area*current , split in different sections.
Salt dilution method. Accurate discharge measurement by adding a salt solution with constant flow Qs. The salt content (dilution) at distance of full mixing is a measure for the natural discharge. Can be used in turbulent streams. Materials: EC-meter, salt, container with constant outflow (mariotte’s bottle; see Wikipedia), stopwatch. Qstream = Qbrine * EC-brine inflow/EC-mix zone (for Qbrine < 0,1* Qstream). Mind EC at equal temperature. (Reference: only my own VU Uelsen instructions 1977)
Salt gulp method: Instant (bucket) input of salt solution and measuring the ‘dilution plume’ in time and area at point of full mixture. Can be used in turbulent streams. Easier than method above. Calculation from time/EC curve (EC curve above natural EC of stream). Q = Mass of salt/(conversion factor * area under curve). Conversion factor is 2.04 at temperature 22 oC. Area in uS/cm * sec. (Reference: Harvey 1993, pg 2.5.2)
Use of a (calibrated) weir or discharge ‘flume’, built in a stream. The height of the water level above the crest is a measure for Q (many formulae). Some in table below (different sources).
-
Weir
Discharge (Q/h relation; m3/s)
Rectangular, wide crested, horizontal (e.g. a dam)
Q = m * W * 1.71 * h1.5;
M about 0.96
Rectangular, sharp with free board
Q = 1.9 *( W-0.2 h)1.5
Triangular, sharp with free board (90o) (Thomson V-notch)
Q= 1.4 * h 2.5
Trapezium, sharp
Q = c * W * h1.5 (c dep of angle)
Cipoletti trapezium: angle 400%; W=bottom width; B >3h
Q = 1.89*W*h1.5
Half circle (e.g. for sewer pipe)
Q = 2.8 * r0.5 * h2
Combination of formulae is possible if the weir is submerge. Example is a V-notch in the center and the a rectangular at the flanks. Other example a lower rectangular wide crest at the center and a higher wide crest at the flanks.
2.2 Indirect flow determination
Flow determination by Manning formulae
The empirical Manning formula is using the characteristics of the wetted cross section, a roughness coefficient for the bottom and the gradient/slope of the stream at that point.
Q = A*v = A / n * R2/3 S1/2
where
Q = discharge (m3/s)
v = cross-sectional average velocity (m/s)
A = cross sectional area of flow (, m2)
n = Manning coefficient of roughness (see table)
R = hydraulic radius ( m) = A/P in which P = wetted perimeter
S = gradient; slope of channel (m/m)
Roughness coefficients (c) can be found in tables. Water levels (minimum, common, maximum) can be obtained from topographical signs or from oral information.
Manning’s coefficient (from Engineeringtoolbox.com)
|
Surface Material |
Manning's
Roughness |
|
Concrete - finished |
0.012 |
|
Earth |
0.025 |
|
Earth channel - clean |
0.022 |
|
Earth channel - gravelly |
0.025 |
|
Earth channel - weedy |
0.030 |
|
Earth channel - stony, cobbles |
0.035 |
|
Floodplains - pasture, farmland |
0.035 |
|
Floodplains - light brush |
0.050 |
|
Floodplains - heavy brush |
0.075 |
|
Floodplains - trees |
0.15 |
Correction factors may be applied for sinuosity of meandering rivers or presence of ripples/banks in river bottom. This is especially relevant at lower stages. In case of floods above the full bank stage, the stream can be divided in different sections with different characteristics (Perimeter and roughness coefficient), e.g. for the central stream bed and for the flow on the flood plains/terraces.
Manning can also be used for overland flow, in which ‘R’ is replaced by flow depth, but there are more accurate formulae for laminar overland flow, like the Friend formulae (Queensland Department of Main Roads 2003, ch 3.5.3.2)
Correlation
Flow can be derived from extrapolation from known discharges in comparable or adjacent water catchments; correction for surface area of catchment. (if catchment is 2 times larger than adjacent catchment, then one might expect flows (average and maximum) to be almost twice the one in this adjacent catchment; except when topography, geology, vegetation are very different).
This method can be used for individual flow estimates and for longer term series (annual flow, peak flow etc), but is less reliable for base flow.
Of assistance can be the Flow correlation method using the ‘Flow Duration Curve’ is a comparable catchment (see chapter 2).
Run off /rainfall ratio
Calculation of run off in relation to precipitation. Q = (Area)n * Rainfall * % of run off (mind dimensions). For annual flows, the ‘power n’ varies mostly between 0.6 and 0.85 with an average of 0.75. For humid climates the value of n is higher. For mean annual flows the ‘n’ is higher than for floods. A low ‘n’ means a rapid decline of Q per surface unit with increase of area. Explanation: Larger areas have more storage capacity and precipitation is not at peak everywhere at same time. Mind, that the precipitation is rarely equal for the entire catchment.
The run-off coefficient is determined by soil, vegetation, topography and rainfall history before the rain event. For longer periods, the coefficient is used for the volume under the hydrograph. For peak flows, the formulae can be used for the height of Qpeak, in case the storm lasts long enough to allow each part of the catchment to contribute to the flow at the outflow point. If Rainfall is expressed as m/s (intensity), then Qpeak (m3/s) = Ratio *P (m/s) * Area (m2)
This method is used for longer periods (like a year), but can also be done for individual rain storm volumes.
For this method, the precipitation data are very important. Good rainfall data are often available at meteorological departments or at Road Works.
Extreme rainfall intensities of 350 mm/hr for a period of 5 minutes is not uncommon (e.g. in Queensland/Australia), but registered extremes are 200 mm/hr for 60 min and 400 mm/hr in 20 minutes.
3 Flow
characterization
Flow characterization/variation includes the determination of the (unit) hydrograph (Q/time curve), minimum flows, mean annual flows and maximum flows.
Q/h relationship
Flow characteristics of a stream can be determined by measuring different flows (Q) at different water levels (h). Q/h relation needs to be established with one of the methods, above.
By measuring the ‘h’ at regular intervals (say daily), one may determine the distribution of the daily flow. For extreme events, however, mostly the Q/h relation is not well known (calibrated) e.g. when a river flows out of its banks. Note that in unstable streams, the Q/h relation changes over time.
A Q/h relationship can be made for a natural river bed. But is can be made much easier and accurate with a weir or a ‘flume’, with pre-defined Q/h relationship. Each model has a mathematically defined relationship. These can be found at internet.
Hydrograph
A hydrograph is the graph in which Q is put against time. It may provide several characteristics, which might be used in correlation studies. Like the steepness with floods and the depletion in periods after/without rain. The depletion is mostly a straight line or a series of straight lines on semi-log paper. In case of a series of straight lines, there are several supplying units (overland storage, bank storage, deeper seepage etc), which are depleted at different speed.
A unit hydrograph describes the typical reaction of a stream on rainfall. A steep front of the hydrograph means a quick response and rapid concentration. A smooth front means a buffering interception or a longer path to reach the outlet. The depletion wing is determined by the depletion coefficient of the joint ‘reservoirs’ contributing to the flow. If put on log paper, the rapid response can be separated from the slow response, and the recharge to the groundwater aquifer (and increase in storage volume) can be measured, being the difference between the old and new depletion curves (or the area between Q0, t0, t1 and Q1, where Q0=Q1 and t0 is the time when the hydrograph starts to climb and t1 is the time, the hydrograph is back at Q0).
Flow Duration Curve
A Flow Duration Curve is a frequency curve, with the discharge in the vertical (expressed as percentage of the average Q; on log-scale) and the exceedance time (percentage of exceedance; on probability paper) in the horizontal. The curve approaches a straight for normal streams. Downcurving means abstraction or leakage or evaporation of swamps/lakes. Up-curving means a prominent slowly reacting groundwater inflow.
Correlation can be easily done with a FDC of a comparable catchment. (flow correlation method). A correlation can be improved by doing some flow measurements in the target stream and the reference stream of which the FDC is known.
A steep FDC means, that it is heavily influenced by storms and rapid inputs. A smooth FDC indicates a large supply from groundwater.
Statistics
Most of the stream characteristics are determined by statistical analysis, using different type of distribution (normal/Gauss, skewed etc) and probability analysis (probability of exceedance or non-exceedance); log relations etc. In many situations, ‘log-normal’ and ‘probability paper’ is used to draw straight graphs. According to Petts and Foster (1983), the availability of paper is more important than a scientific ally sound choice!
4 Minimum
flows
Minimum flows are important to know the minimum capacity for supply. For seasonal rivers, the duration of non-flow is important.
Duration of non-flow
The duration of absence of flow is the period for which water might need to be stored. It is important to collect information about the historical data on length, to make a probability analysis. Mostly the 1/10 years or 1/20 years length is taken for design purposes. Such an analysis assumes the absence of a climate trend. Attention needs to be given for situations with two dry seasons in a year. Then it could be good to analyse the data separately.
Duration of dry season
Dry months are mostly defined as months in which Rainfall is below a percentage of Potential Evapotranspiration. But in some cases an absolute rainfall maximum is used. The British Institute of Hydrology uses a daily threshold of 0.3 mm, which is about 10% of the PE in summer.
This period is often a measure for the period without flow in seasonal rivers.
Of statistical importance are the average length and the once in 10 or 20 years long dry season.
The statistical distribution can be very skewed, especially when some of the years have no dry months at all. A complicating factor is arrived, if a wet season has not got a month with enough rainfall (above the established threshold).
Base flow
The once in 10 years minimum flow can be determined in two ways. One is by statistical analysis if there are sufficient years in which the flow was measured. If this is not the case, then the depletion curve needs to be determined (which can be done by a few flow measurements during the dry season), combined with the duration of drought analysis (above).
The base flow is shown as the depletion curve in the hydrograph and represents the inflow from groundwater to the stream. The outflow of an aquifer is characterized as Qt = Qo * e -(t/k) . It gives a straight line on semi-log paper, in which k is the inverse of the time period for 1 one e-log cycle reduction of Q..
If the depletion curve in a hydrograph is flattening over time, it means that there were more aquifers contributing, but they might dry up one after the other. The most ‘slow depletion’ will continue for the longest period. Mind that the Storage volume at moment ‘t’ of each aquifer can be derived from this depletion factor ‘k’: S = k*Qt..
If the depletion curve in a hydrograph steepens over time, it means that there is abstraction somewhere (infiltration in river bed, high evaporation in a swamp, abstraction for irrigation etc).
The once in ten years low flow in a perennial stream is determined by the length of the one in ten years dry period (see above), and the depletion curve from the start of the dry season.
Bouman made for small mountain catchments along the escarpment of Southern Morogoro Region (Tanzania) an analysis and made a map which showed the once in 10 years base flow, expressed in l/s/km2. (DHV 1983).
5 Annual
flows
The annual flow is a measure for the entire volume of run off from a defined catchment. It is normally expressed in m3/s or l/s. The annual volume (m3) is then 365*24*3,600 =31.5 106 times the m3 flow per second.
The annual flow volume can also be expressed in run off ‘depth’ (in mm or l/m2), meaning the total volume divided by the surface area of the catchment. In this way it is easy to compare with the precipitation.
In a Flow Duration Curve, the mean annual flow is normally exceeded in less than 50% of the time. This is because of the slow depletion at lower discharges. (it is somewhere between 20 and 35%).
Frequency graphs of annual flows normally show a rather symmetrical distribution.
For uniform catchments, the annual flow per unit area reduces with the area: Q = c * An, where n < 1.
This is because in larger catchments, there is more potential for storage (and evaporation). The factor n is normally between 0.65 and 0.8 with an average of 0.75. The factor is high in humid climates and low in semi-arid.
The (mean) annual flow can be expressed in function of area (A), Precipitation (P) and a area specific factor (c).: Q = c * P * A.
The factor c is also known as the rainfall/run off ratio. For small catchments without intermediate storage the ratio is dependent on the Evapotranspiration and Infiltration/Recharge.
According to the water balance, Run off + Evapotranspiration + Infiltration/Recharge = Precipitation. As Evapotranspiration and Infiltration/Recharge are rather constant over the years, variation in Precipitation is almost directly translated into variation in run off. Hence, the use of a constant factor ‘c’ is more applicable for mean annual run off than for the run off of individual years.
For West Africa, ORSTOM published many hydrological characteristics, like probability graphs for annual run off for different soil types and catchment sizes.
6 Floods
Flood levels can be recorded by local people, often with the year of occurrence. This oral data bank can be the best source for flood analysis. Manning’s formulae can be of use to do a quick analysis of peak flows and their frequency. Manning’s formulae, or the formulae for a wide crested rectangular weir can be of use to forecast the new flood level after constructing a new structure, like a checkdam or a sand dam.
Like the annual flow, the flood extremes can be expressed both in ‘depth (mm; l/m2) or total volume (m3)’ and in ‘peak flow (m3/s)’. The first (depth or volume) is easier to estimate and relevant to determine the storage characteristics of a reservoir. The latter is important, as it determines maximum flood levels, for which the ‘structures’ need to be protected by anchor walls and spill ways of good capacity.
For a river system with a river bank and flood plains, the bank full stage repeats every 1 – 2 years. The once in 50 years flood is about 1.8 times the height of the bank full stage. Terrace levels may indicate the frequency of different floods. (Meijerink 1970).
When analyzing annual flood frequency, there seems to be little difference whether one takes all the floods above a certain threshold (say the mean annual flood) or the highest flood in each hydrological year. (Meijerink 1970)
The rainfall ‘history’ of a catchment is an important condition for flood generation. If an area is still dry, a lot of rainfall is absorbed by the soil and intermediate storage and floods are less pronounced. But if all soils are saturated from previous storms and storage/buffers are full, response may be high.
For floods in one catchment, the discharge diminishes considerably with the surface area. Q = c * An, in which n < 0.7. The reason for this is that the peak precipitation is rarely equal over the entire catchment (especially not for larger catchments) and in larger catchments, interceptive storage (e.g. flood plains) or high infiltration areas are found.
Depth or volume of floods
For the determination of the Volume or depth the so called Curve Number method is often applied. In this method, the catchment is subdivided in sub-units with uniform run off producing characteristics, expressed in a CN (Curve Number). For each unit the mean Precipitation is established. From these variables, the Run off depth is determined. The Flood volume at the outlet is ∑ Qi.Ai

Curve
Number method for estimating excess precipitation. (source)
The CN is listed in the table below. These CN’s are for moderate pre-conditions. If the pre-conditions were very humid, the CN should be increased. If it was very dry, it should be reduced.
This Curve Number method uses both the initial interception, its reduction in time and the final run off coefficient, based on soils and vegetation.
Curve Numbers as a function of land use and soil condition (source)

Kruseman/De ridder in ILRI 1973 publication mention another method: the coaxial rainfall-recharge diagram, using the Antecedent Precipitation Index, Seasonal index, duration of rain, depth of rain to determine the basin recharge and (indirectly) the run off.
Flood peaks
For the determination of Peak Floods, the Rational Method is normally applied.
For minor catchments, the maximum flood at the outlet point occurs when each part of the catchment contributes to the flow at the outlet point (at time of concentration), and when rainfall ‘history’ already saturated the soils and intermediate storage facilities. In that case the Rational Method is applied in which Q = c * Pi * A. If A = 4 km2 , rainfall intensity is 0.02 mm/sec and c = 0.6 (60% of rainfall is run off), then Q = 0.6 * 0.00002 * 40.000 = 48 m3/sec.
The idea is, that just at this moment of time of concentration the maximum is reached, because potential rain intensity reduces quickly with time.
Bransby and Williams also developed a formula for the time of concentration, which can be computed at this website.
Queensland Department of Main roads provides several formulae for time of concentration (chapter 3.5.3.2).
Rasmussen provides a table for run off coefficients.
Rational method runoff coefficient (source)

More complex coefficient determination is developed by Bransby and Williams, based on 5 parameters: rainfall intensity, relief, surface interception/retention, soil infiltration capacity and cover (Meijerink 1970).
Also Cook developed a similar coefficient system based on 4 parameters (excluding the rainfall intensity) and made for the Upper Mississippi Catchment probability graphs for different coefficients. (Meijerink 1970).
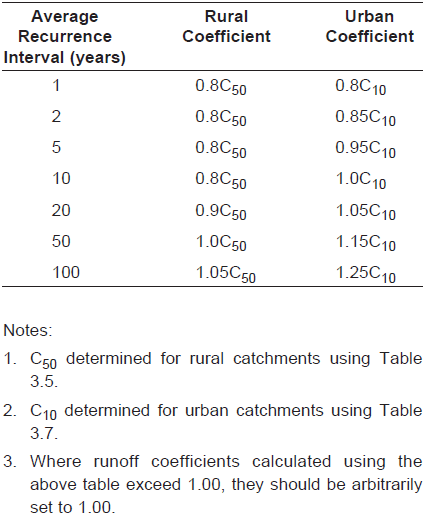
Queensland Department of Main roads (2003, chapter 3.5.3.4) has elaborated the coefficients for different probability frequencies.
In their tables 3.5 and 3.7, the coefficients for rural (recurrence 50 years) and urban (recurrence 10 years) are elaborated. Table 3.8 provide the adjustment figures for other probabilities.
(see next pages)
It needs to be said that all these methods are empirical and not always very accurate. To mention one example: catchments with a long shape have lower peaks than concentric catchments, where peak flows from each tributary coincide.
If catchments become larger, the calculation becomes much more complicated as not each part is contribution at the same time at the same intensity. For a certain area, An can still be applied (n = <0.7), but for larger areas, also the intensity has to be lowered and the ‘c’ because of intermediate storage in flood plains. Queensland Department of Main roads refers in this case to the Departments Form M2759 for Bridge Waterways.
For very large catchments, the high intensity storms in one area may not occur in the other. In that case, a flood wave moves downward without being fed by new water. Flood routing is applied in such conditions. (Reference: Rasmussen Ch 7.2 pg 9 -14).
Estimation of the runoff coefficient for rural catchments (source)

C10 Values (source)

Adjustment factors for runoff coefficients for other average rucurrence intervals (source)
Remark:
Flows of more than 0.15 m/s are erosive for (loose) sands. Flows of over 0.5 m/s are also erosive for clays and gravels. See figure from Meijerink 1970.

Flow
velocities, erosion, transportation and sedimentation for different
grain sizes.


